Skip to main content

The Foolproof Way to Divide Paper Into N'ths

We all have been there... asking how to divide paper into 14ths or 15ths and occasionally got the answer of "just make 16 grid and cut it". Another scenario is being terrified with prime number division like 13ths or 17ths. In reality it's not that difficult. This post will share how to make such division just inside your head so you can start folding right away. I promise it won't require any arcane maths.

Theory

Dividing paper into \(N\)'ths can be simplified into splitting the paper's edge into \(a : b\), where \(a+b=N\). Let's start with the case where \(N\) is an odd number.

For instance, to get \(N=5\), you can use:
  • \(a=1\) and \(b=4\), or
  • \(a=2\) and \(b=3\).
Using \(a=3\) and \(b=2\) or beyond is essentially the same as the previous options so don't bother with it.
It is good to have \(a\) and \(b\) not in the extremes, like one is far smaller than the other, to avoid narrow triangle which is difficult to fold.

To divide paper into \(a : b\), we can use the triangle congruence property. Imagine you have a triangle that lies on a surface. If you slice that triangle horizontally on a certain height from the surface, the proportion of the top half of the triangle will remain the same as before.
The shaded triangle has the same proportion.

Let's begin the operation to divide the paper.

First, find a number that is larger or equal than \(a\) and \(b\) that we will call \(x\). Any number is fine but it would be much easier to use power of 2, like 2, 4, 8, 16, etc.

Second, mark the paper's top edge for \(\frac{a}{x}\) from left, and \(\frac{b}{x}\) from right.
This is why we want \(x\) to be power of 2, because it is easy to repeatedly do selective division the top edge into 2 to locate \(\frac{a}{x}\) and \(\frac{b}{x}\). In the paper, this is done by doing small valley fold or pinching.

Black mark shows where \(\frac{a}{x}\) is from the left.
White mark shows where \(\frac{b}{x}\) from the right.

Lastly, draw (or fold) a line from \(\frac{a}{x}\) towards farther corner in the bottom edge. Do the same for \(b\). The intersection will divide the paper into \(a : b\) horizontally.
Dashed lines divide the paper into \(a : b\).

How do we know that the intersection divides the paper into \(a : b\) horizontally?
Observe the image below.
Shaded triangles show the congruence property in action.
\(\Delta PQR\) and \(\Delta VXR\) are congruent. 

We initially have two triangles, \(\Delta PQR\) and \(\Delta STU\). They are shrunk together into \(\Delta VXR\) and \(\Delta XWU\), with both of them touching the intersection \(X\). The ratio of \(PQ\) and \(ST\) is maintained in \(VX\) and \(XW\) thanks to the congruence property, so we know that \(VX : XW\) is equal to \(\frac{a}{x} : \frac{b}{x}\), or simply just \(a : b\).

From here, you should be able divide the paper into \(N\)'ths easily.

Examples

Let's take a look at how to divide paper into 5ths.
Use \(a=1\), \(b=4\), \(x=4\), and we get this:
You can further divide the right side into four equal parts to get 5ths division.

Alternatively, we can use \(a=2\), \(b=3\), \(x=4\):
To full get 5ths division, first divide the left side into two. Then use that crease to divide the right side into 3rds. Hint: valley fold the right edge into 1/2 of the left side.

Let's try it again for 17th. We could use \(a=1\), \(b=16\), \(x=16\), and we'll get this:

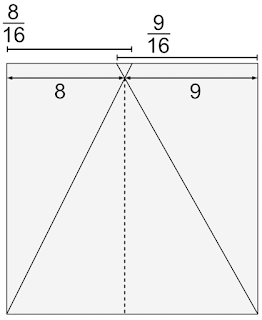
It works in theory, but in practice it is difficult to fold such a narrow triangle to connect \(\frac{1}{16}\) to bottom left corner accurately. A better combination is \(a=8\), \(b=9\), \(x=16\). This is what Kamiya used for his spinosaurus reference.

This method works well up to 31sts division. For odd division after that, maybe just use ruler.

Even Number

If \(N\) is even number, then divide it by 2 until it is odd, and proceed to perform the procedure above for that odd number. Let \(k\) be the amount of times such division happened. The final step is just to divide each unit by half \(k\) times.

For example, say that we want to divide the paper into 44ths. To get odd number, we divide 44 by-2 two times, which result in 11. Once we divide the paper into 11ths, all we need to do is to divide each unit by-2 two times.

Exercises

Try to conceptually divide paper into 3rds, 7ths and 13rds.

We can extend this idea to locate \(a + b\sqrt{2}\) reference, which is the basis of how Kamiya did it on his website. I will leave that out to you as an exercise.
Labels:

Comments

Post a Comment

Popular posts from this blog

Origami Frigatebird v3

My frigatebird's color is fading, so I thought about refolding it with something better than double tissue. While doing so, I got some ideas to update it. Now it has distinction of lower/upper beak, and individual toes. Also used this opportunity to fold the female version.
Post a Comment
Read more

Origami Turkey Vulture

Turkey vulture is a type of vulture whose head and color just happened to look like wild turkey. I frequently see them in San Jose and its surrounding wilderness, slowly soaring and gliding on low altitude. Their V-shaped pose with occasional wobble is rather unique, so it is easy to identify them.
Post a Comment
Read more

Origami Crocodile

A simple crocodile foldable with any regular paper in 15 minutes.
Post a Comment
Read more

Origami Proboscis Monkey

Adult male proboscis monkey has a large nose that dangle below the mouth. It's like Squidward. Apparently it's used for producing sound and natural selection prefer the louder one. Image credit:  https://eol.org/pages/310436 It is endemic to Borneo and is critically endangered. Coincidentally a comrade in Origami Dan, Naoki , asked me to join force for raising awareness on endangered species. From now on, my every design with endangered species will have the red stamp with tarsier face.
Post a Comment
Read more

Warped and Wrinkled Paper Curse

After starting using Carboxy Methylcellulose (CMC), I began to wonder if my setup wasn't right. The problem was my double tissue would always peel itself when drying. There will be high pitched popping sound from the paper every now and then. Finally it would be completely off the surface. Whereas on every tutorial I saw, the paper will still stick to the surface and we have to peel it off. The bad part is the paper will be warped; it's not flat. It is difficult to fold a straight line on paper like this. Imagine precreasing a grid or locating references when your fold can be bent due to the paper's bump. I have theory on why the warp happened. Before going to that, it is important to know that: When a paper is wet, it expands. When it dries, it will return to the original size. However it will keep its shape when it is wet, meaning that if it is bent when wet, it will retain that bend when dried.  When my paper dried partially, that region will shrink. This created differe...
Post a Comment
Read more